Stunning ultra-high diamond thermal conductivity

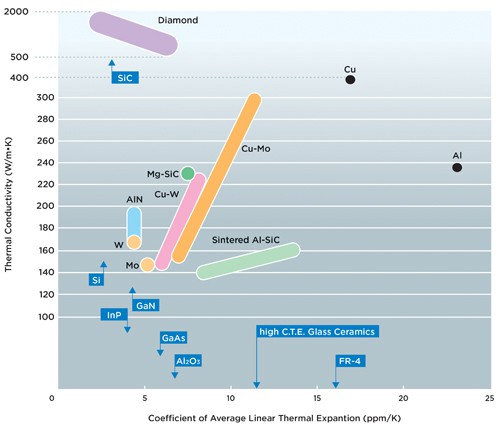
Diamond is unmatched as a thermal conductor.   It   is   informative   to   compare   the   thermal   conductivity   of diamond to that of other materials with which   it may be used or with which   it may compete. Polycrystalline diamond films of good quality generally exhibit thermal conductivity in the direction of growth of 55% of single crystals，but these figures are dependent on grain size .

Heat may be transferred in a solid principally by one of two mechanisms. The most common mechanism, drifting electrons, is most prevalent in metals and alloys.   The second principal mechanism is that of thermal phonons (i.e., the directional wave motion of interacting lattice ions).   This mechanism is most prevalent in dielectrics such as diamond.   At low temperatures, thermal conduction is limited by phonon scattering from impurities and defects in a manner similar to metals.   Small sample size may also affect thermal conductivity as phonon phase cancellation from sample boundaries becomes significant.   Boundary scattering certainly affects most of the published data for the thermal conductivity of diamond at low temperatures.   Actual values are thought to be considerably higher than those published.   Diamond’s extraordinary thermal conductivity is entirely due to thermal phonons.

At higher temperatures, phonon-phonon scattering predominates; therefore the thermal conductivities of many dielectrics tend to converge at high temperatures.   Phonons may also be scattered by isotopic variations.   Carbon naturally contains about 1% of the C13 isotope. While the mass differential between Si28 and Si29 is only 3.6%, the mass differential between C12 and C13 is 8.3%.   Diamond synthesized from isotopically pure carbon increases its thermal conductivity by 40% over natural diamond .

In work by Novikov et al. The thermal conductivity of single diamond crystals and CVD diamond films with different C13 isotope content has been analyzed in the framework of Debye’s model using Klemens–Callaway’s expression [5] for the thermal conductivity.   The increase in thermal conductivity for isotopically pure diamond can be explained by Callaway’s model by lowering the isotope-scattering effect (Figure 2‑2).   The effect of C13 isotopes on the diamond thermal conductivity was considered, with allowance made for the earlier assumption that the presence of isotopic impurity, apart from direct resistive effects, results in the activation of the normal phonon scattering processes. As a result, the relaxation time of normal processes is observed to depend on the isotopic concentration. In this case, a good agreement between theory and experiment is observed for the temperature region 10 – 1000 K.

Maximum thermal conductivity is essential for thermal management applications.   It is also of secondary importance for wear coatings that generate heat during use.   With unmatched thermal conductivity, diamond appears to be the ideal heat exchange material. It may be thought of as a solid state heat pipe, but capable of operating over a much wider range of temperatures than any liquid heat pipe.   Data from several investigators have shown that minimizing non-diamond material leads to better thermal conductivity.

A lesser known aspect of diamond’s thermal conductivity is it’s strong temperature dependence which increases dramatically above its already extraordinary room temperature values when used at cryogenic temperatures. At -150C, diamond’s thermal conductivity exceeds 5,000 W/mK.

We focus on the research and production of diamond, provide diamond heat sinks and other products, welcome to negotiate.